In many computational problems – such as pathfinding, game playing, robotics, and optimization—the search space can be extremely large. Exploring all possible solutions exhaustively is often impractical or impossible. Heuristic search addresses this challenge by using additional knowledge, called heuristics, to guide the search process toward promising solutions more efficiently. Two of the most well-known heuristic search algorithms are Greedy Best-First Search and A* (A-star) search. This article introduces the concept of heuristic search and explains how these two algorithms fit into it.
What Is Heuristic Search?
A heuristic search is a search strategy that uses a heuristic function to estimate how close a given state is to a goal state. Instead of blindly exploring the search space, heuristic search algorithms make informed decisions about which node to explore next.
A heuristic function is commonly denoted as:
h(n)
where:
- n is a node (or state)
- h(n) estimates the cost or distance from n to the goal
Heuristic search is also known as informed search, in contrast to uninformed search methods like Breadth-First Search or Depth-First Search, which do not use domain-specific knowledge.
Maze Example
To explain the Greedy Heuristic a Maze example is chosen. In a Labyrinth the goal is to find the exit (e) from a starting point (s) efficiently without having a lot of loops or turns.
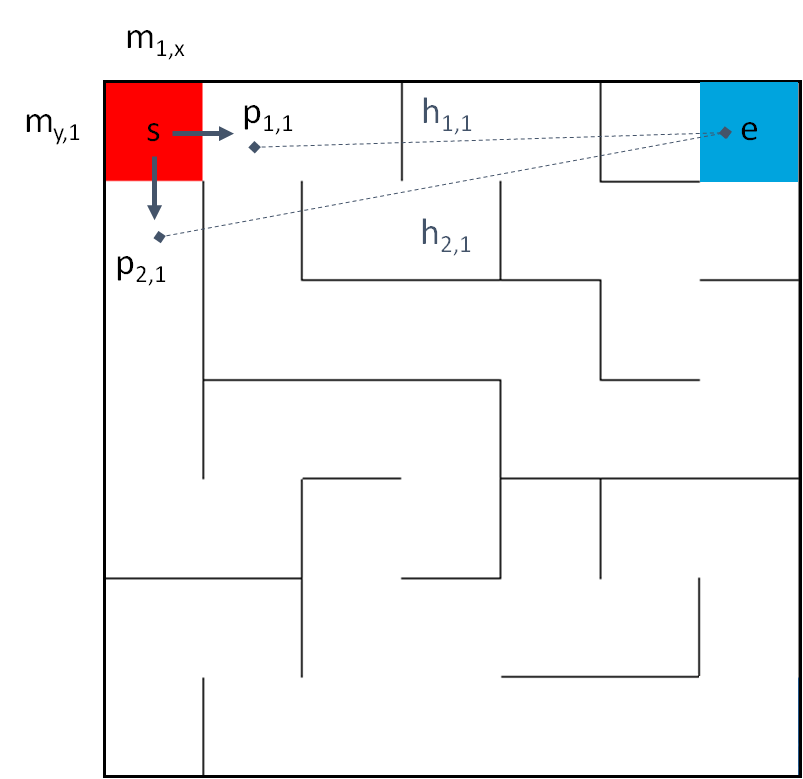
To judge about the next step of path finding following heuristic calculation for this example is taken
f_{(n,k)} = h_{(n,k)} = \big|\vec{p}_{n,k}-\vec{e}\big|=\sqrt{(e_x-p_{x(n,k)})^2+(e_y-p_{y(n,k)})^2}So the heuristic calculation is equal to heuristic function since no more further calculation to consider. To find the best solution the minimum distance between the next steps and the exit has to be selected.
f_{min(k)} = h_{min(k)} =\min_{\substack{n=0,..N-1}}\Bigg\{\big|\vec{p}_{n,k}-\vec{e}\big|\Bigg\}However, it is important to note that greedy algorithms do not always guarantee an optimal solution for every problem. In some cases, a greedy approach may lead to a locally optimal solution that is not globally optimal. The lack of backtracking or reconsideration of previous choices can cause the algorithm to overlook potentially better solutions that require a more in-depth exploration of the solution space.
Decision Tree
Based on the Maze example introduced above for every position my,x reached a state in a decision tree is represented. The connection between the states is represented by the heuristic calculation h(n,k).
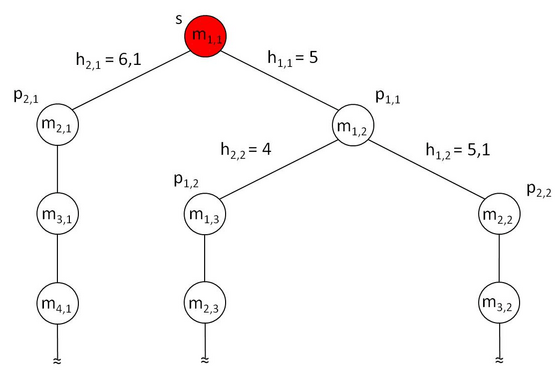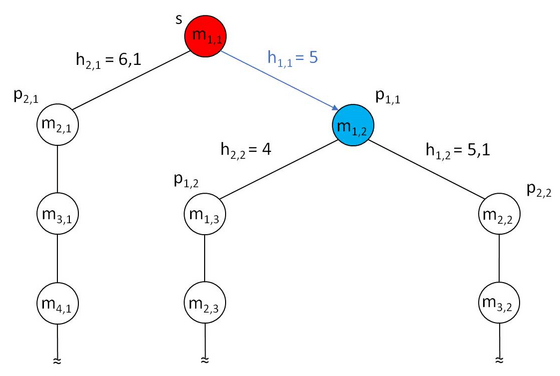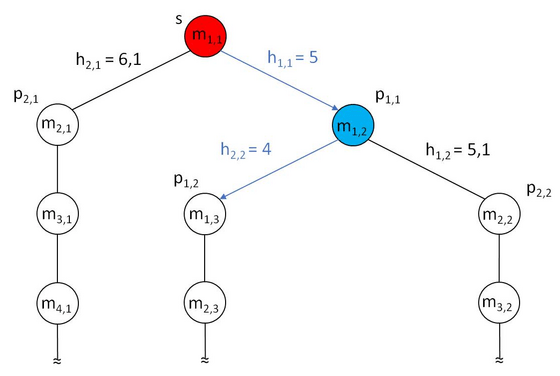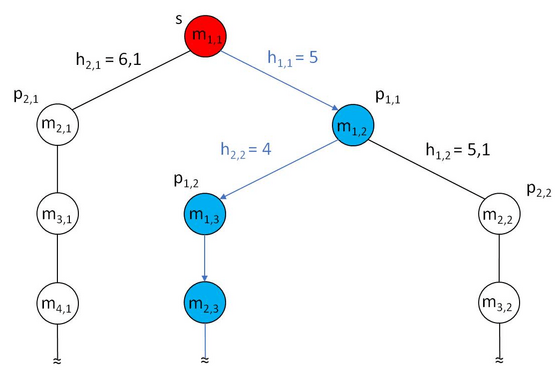
Based on the minimun heuristic result the connection is selected to move to next step. This is repeated until exit state (e) is reached.
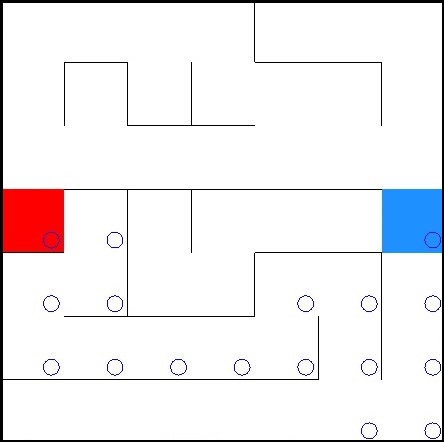
As shown above the Greedy Algorithm starts to the right based on the minimum heuristic calculation and then follows the path until exit has been found. Note that there is no backtracking to try another route. This would cost more time and sometimes even inefficient.
Optimal Solution
The Greedy algorithm doesn’t consider the effort needed to reach actual position and to reach exit finally. Thus the effort is another information which can be added to the heuristic.
f_{(k)} = h_{(k)} + c_{(k)}=\big|\vec{p}_k-\vec{e}\big|+\big|\vec{s}-\vec{p}_k\big|\\[5pt]This defines an optimal search algorithm and is named as A* algorithm (A star algorithm). So the total effort over time and steps is finally the sum of the costs (c).
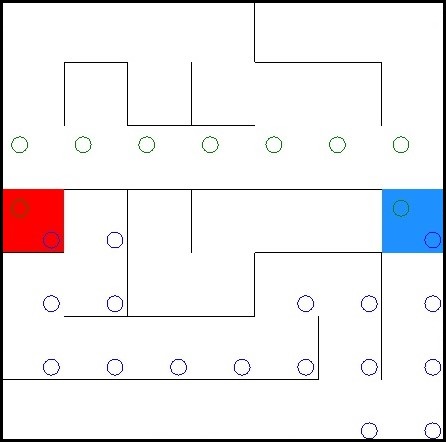
The result in opposite of the Greedy Algorithm is visible by the example used above. The path with blue circles was calculated by the Greedy Algorithm and the green circle ones by the A* Algorithm.
Implementation in C#
The following section shows the C# implementation for Greedy and A* Algorithm. The complete source code is available in Github.
There is a abstract class “Route” which provides common functions used by both algorithms except “find_children” function.
abstract class Route
{
protected PointF calcRoomPos(int room) { ... }
protected double distance(pos_t room1, pos_t room2) { ... }
protected int compareCostBySum(cost_t a, cost_t b) { ... }
protected int applicable(pos_t start, ref pos_t next, pos_t destination, ref double cost, ref double heuristic) { ... }
protected abstract int find_children(pos_t start, pos_t destination, int index);
public Route() { ... }
public void clearRoute() { ... }
public virtual void routeStart(int actR, int tarR, Size roomC, List<Door> doorL) { ... }
public virtual void routeProcess() { ... }
}This function (find_children) is implemented in separate classes for Greedy (GreedyRoute) and A* (AStarRoute) derived from base class Route based on their own heuristic calculations.
class GreedyRoute : Route
{
public GreedyRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index) { ... }
}
class AStarRoute : Route
{
public AStarRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index) { ... }
}The function “calcRoomPos” calculates the middle position of a maze field based on the field number. Here mentioned as room.
protected PointF calcRoomPos(int room)
{
PointF ret = new PointF();
ret.X = (((float)(room % rooms.Width)) * roomWidthLen) + (roomWidthLen / 2.0f);
ret.Y = (((float)(room / rooms.Height)) * roomHeightLen) + (roomHeightLen / 2.0f);
return ret;
}The distance between two maze fields e.g. actual position and exit field is calculated by theorem of pythagoras.
protected double distance(pos_t room1, pos_t room2)
{
double ret;
double x1 = room1.pos.X;
double y1 = room1.pos.Y;
double x2 = room2.pos.X;
double y2 = room2.pos.Y;
ret = Math.Sqrt(((x1 - x2) * (x1 - x2)) + ((y1 - y2) * (y1 - y2)));
return ret;
}The order of the sort algorithm to take next maze field is given by following function. Note that in case of equal costs the order of next maze field is decided by random. The variable “sum” contains in Greedy Algorithm the guess (cost from actual position to exit field) and in A* Algorithm the effort plus guess (total costs).
protected int compareCostBySum(cost_t a, cost_t b)
{
int ascend = -1;
if (a.sum > b.sum)
{
ascend = 1;
}
else
if (a.sum == b.sum)
{
//ascend = 0;
ascend = 1;
var random = new Random(Guid.NewGuid().GetHashCode());
if (random.Next(2) == 0)
{
ascend = -1;
}
}
return ascend;
}The function “applicable” checks whether next maze field is a valid field to be reached. A valid field here means a transition is possible.
protected int applicable(pos_t start, ref pos_t next, pos_t destination, ref double cost, ref double heuristic)
{
int i;
int size = doorList.Count;
if (start.room == next.room)
{
return 0;
}
for (i = 0; i < size; i++)
{
if (((doorList.ElementAt(i).Cell1 == start.room) || (doorList.ElementAt(i).Cell2 == start.room))
&&
((doorList.ElementAt(i).Cell1 == next.room) || (doorList.ElementAt(i).Cell2 == next.room)))
{
next.pos = calcRoomPos(next.room);
cost = distance(start, next);
heuristic = distance(next, destination);
return 1;
}
}
return 0;
}The route calculation will be started by “routeStart” function common for both algorithms. All variables, lists, etc. will be initialized or reset to be started from scratch.
public virtual void routeStart(int actR, int tarR, Size roomC, List<Door> doorL)
{
route_cost = 0;
route_list.Clear();
routes.Clear();
search_route_list.Clear();
cost_list.Clear();
if (tarR == 0)
{
return;
}
startRoom = actR;
actRoom = actR;
tarRoom = tarR;
rooms = roomC;
doorList = doorL;
pos_t startpos;
startpos.room = actRoom;
roomWidthLen = (100.0f / ((float)rooms.Width));
roomHeightLen = (100.0f / ((float)rooms.Height));
actPos = calcRoomPos(actRoom);
startpos.pos = actPos;
tarRoomPos.room = tarRoom;
tarPos = calcRoomPos(tarRoom);
tarRoomPos.pos = tarPos;
route_list.Add(startpos);
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = route_list.Last();
knotRoom.actualCost = 0.0f;
knotRoom.done = false;
knotRoom.childrenRooms = new List<search_route_t>();
search_route_list.Add(knotRoom);
finished = false;
}The actually algorithm is running in “routeProcess”. This function is called cyclically. It consists of a main if, else-if, else condition. The first if condition checks whether to go back from a dead end. The else-if condition is true as long as there is the exit field is not reached yet and finally in else condition the exit field was found.
public virtual void routeProcess()
{
if (search_route_list.Last().done == true)
{
route_list.RemoveAt(route_list.Count - 1);
search_route_list.RemoveAt(search_route_list.Count - 1);
if (search_route_list.Count > 0)
{
search_route_list.Last().childrenRooms.RemoveAt(search_route_list.Last().childrenRooms.Count - 1);
}
int childrensCount = 0;
if (search_route_list.Count > 0)
{
childrensCount = search_route_list.Last().childrenRooms.Count;
}
if (childrensCount > 0)
{
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = search_route_list.Last().childrenRooms.Last().actualRoom;
knotRoom.actualCost = search_route_list.Last().childrenRooms.Last().actualCost;
knotRoom.done = false;
knotRoom.childrenRooms = new List<search_route_t>();
// New active knot
search_route_list.Add(knotRoom);
search_route_list.Last().done = false;
route_list.Add(search_route_list.Last().actualRoom);
}
else
{
// No more children
bool toBeFinished = false;
if (search_route_list.Count > 0)
{
search_route_list.Last().done = true;
if (search_route_list.Last().actualRoom.room == startRoom)
{
toBeFinished = true;
}
}
else
{
toBeFinished = true;
}
if (toBeFinished == true)
{
if (routes.Count > 0)
{
// All solutions found
Debug.WriteLine("All Routes found\n");
int minRoute = 100000;
int index = 0;
for (int i = 0; i < routes.Count; i++)
{
int newMin = routes.ElementAt(i).Count;
if (newMin < minRoute)
{
minRoute = newMin;
index = i;
}
}
route_list.Clear();
route_list = routes.ElementAt(index);
finished = true;
}
else
{
Debug.WriteLine("No Routes found\n");
}
}
}
}
else
if (search_route_list.Last().actualRoom.room != tarRoom)
{
int n;
int found = 0;
cost_list.Clear();
found = find_children(search_route_list.Last().actualRoom, tarRoomPos, 0);
if (found > 0)
{
cost_list.Sort(compareCostBySum);
for (n = found - 1; n >= 0; n--)
{
search_route_t foundroom = new search_route_t();
foundroom.actualRoom = cost_list[n].room;
foundroom.actualCost = cost_list[n].value + search_route_list.Last().actualCost;
foundroom.childrenRooms = new List<search_route_t>();
search_route_list.Last().childrenRooms.Add(foundroom);
}
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = search_route_list.Last().childrenRooms.Last().actualRoom;
knotRoom.actualCost = search_route_list.Last().childrenRooms.Last().actualCost;
knotRoom.childrenRooms = new List<search_route_t>();
// New active knot
search_route_list.Add(knotRoom);
search_route_list.Last().done = false;
route_list.Add(search_route_list.Last().actualRoom);
}
else
{
// New active knot has no children
// Remove knot
search_route_list.RemoveAt(search_route_list.Count - 1);
search_route_list.Last().childrenRooms.RemoveAt(search_route_list.Last().childrenRooms.Count - 1);
route_list.RemoveAt(route_list.Count - 1);
if (search_route_list.Last().childrenRooms.Count > 0)
{
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = search_route_list.Last().childrenRooms.Last().actualRoom;
knotRoom.actualCost = search_route_list.Last().childrenRooms.Last().actualCost;
knotRoom.childrenRooms = new List<search_route_t>();
// New active knot
search_route_list.Add(knotRoom);
search_route_list.Last().done = false;
route_list.Add(search_route_list.Last().actualRoom);
}
else
{
// No more children
search_route_list.Last().done = true;
}
}
}
else
{
routes.Add(new List<pos_t>(route_list));
route_cost = search_route_list.Last().actualCost + distance(search_route_list.ElementAt(search_route_list.Count - 1).actualRoom, tarRoomPos);
Debug.WriteLine("Route cost: " + route_cost.ToString());
for (int i = 0; i < route_list.Count; i++)
{
Debug.Write(route_list.ElementAt(i).room.ToString() + ' ');
}
Debug.WriteLine("\n");
search_route_list.Last().done = true;
}
}Coming now to Algorithm specific “find_children” implementations. The main difference is the calculation of the cost. In Greedy Algorithm the cost is defined by the distance to exit field (guess) and in A* Algorithm the cost is defined by the distance to exit field plus the effort spent from start to actual position (guess+effort).
class GreedyRoute : Route
{
public GreedyRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index)
{
int i;
double effort = 0.0;
double guess = 0.0;
int size = (rooms.Height * rooms.Width);
for (i = 0; i < size; i++)
{
pos_t next;
next.room = i + 1;
next.pos = new PointF(0, 0);
if (applicable(start, ref next, destination, ref effort, ref guess) != 0)
{
int found = 0;
for (int j = 0; j < route_list.Count; j++)
{
if (route_list.ElementAt(j).room == next.room)
{
found = 1;
break;
}
}
if (found == 0)
{
cost_t cost;
cost.room.room = next.room;
cost.room.pos = next.pos;
cost.value = effort;
cost.sum = guess;
cost_list.Add(cost);
}
}
}
return cost_list.Count;
}
}class AStarRoute : Route
{
public AStarRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index)
{
int i;
double effort = 0.0;
double guess = 0.0;
int size = (rooms.Height * rooms.Width);
for (i = 0; i < size; i++)
{
pos_t next;
next.room = i;
next.pos = new PointF(0, 0);
if( applicable(start, ref next, destination, ref effort, ref guess) != 0)
{
int found = 0;
for (int j = 0; j < route_list.Count; j++)
{
if (route_list.ElementAt(j).room == next.room)
{
found = 1;
break;
}
}
if (found == 0)
{
cost_t cost;
cost.room.room = next.room;
cost.room.pos = next.pos;
cost.value = effort;
cost.sum = effort + guess;
cost_list.Add(cost);
}
}
}
return cost_list.Count;
}
}Conclusion
Heuristic search plays a central role in artificial intelligence by enabling efficient exploration of large and complex search spaces. Greedy Best-First Search prioritizes speed by relying solely on heuristic information, while A* search achieves optimal solutions by combining heuristic guidance with actual path costs. Choosing between these approaches depends on the problem requirements—whether speed or optimality is more important. With a well-designed heuristic, heuristic search algorithms can dramatically outperform uninformed search methods and make otherwise intractable problems solvable.
