In the world of computer science and optimization, the term “greedy algorithm” refers to a powerful and widely used approach for solving various computational problems. A greedy algorithm is an algorithmic paradigm that makes locally optimal choices at each step with the hope of finding a global optimum. In other words, it seeks to make the best decision at each stage without worrying about the future implications, often leading to an efficient and feasible solution.
The fundamental idea behind a greedy algorithm is relatively straightforward. At each step of the algorithm, it selects the best option available based on some criterion, regardless of how this decision may affect future steps. This strategy is known as the “greedy choice property.” The algorithm continues this process until it has reached a solution that is considered satisfactory.
Greedy algorithms are particularly useful for solving optimization problems where the goal is to maximize or minimize a certain objective function. They are often employed in situations where a global optimal solution is not required, and a near-optimal solution that can be found efficiently is sufficient.
One of the main advantages of greedy algorithms is their simplicity and efficiency. Unlike some other optimization techniques that require complex computations, a greedy algorithm is generally easy to understand and implement. Moreover, it can often provide a solution in a relatively short amount of time, making it suitable for real-time or resource-constrained applications.
Maze Example
To explain the Greedy algorithm a Maze example is chosen. In a Labyrinth the goal is to find the exit (e) from a starting point (s) efficiently without having a lot of loops or turns.
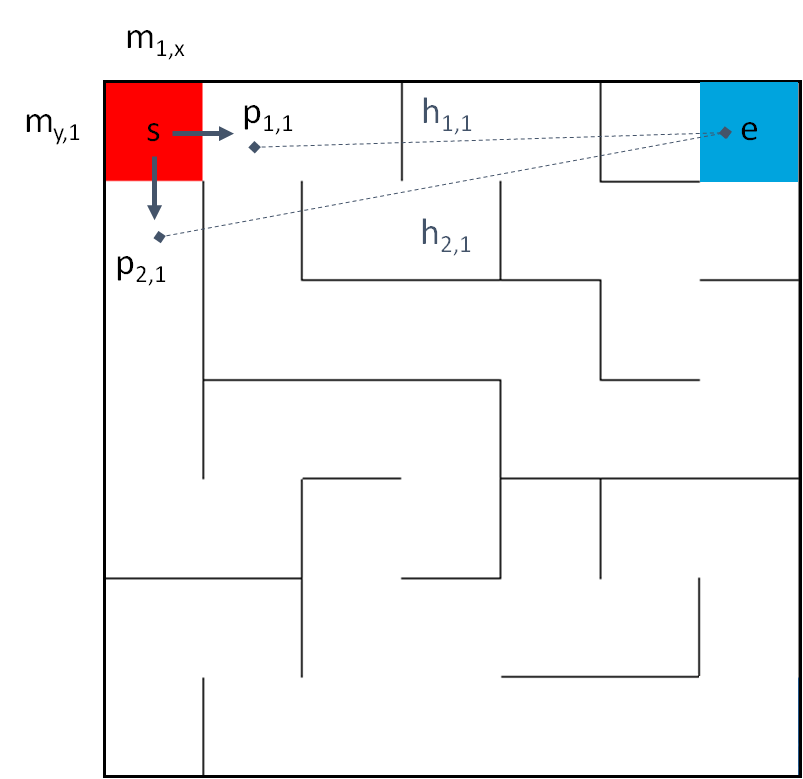
To judge about the next step of path finding following heuristic calculation for this example is taken
f_{(n,k)} = h_{(n,k)} = \big|\vec{p}_{n,k}-\vec{e}\big|=\sqrt{(e_x-p_{x(n,k)})^2+(e_y-p_{y(n,k)})^2}So the heuristic calculation is equal to heuristic function since no more further calculation to consider. To find the best solution the minimum distance between the next steps and the exit has to be selected.
f_{min(k)} = h_{min(k)} =\min_{\substack{n=0,..N-1}}\Bigg\{\big|\vec{p}_{n,k}-\vec{e}\big|\Bigg\}However, it is important to note that greedy algorithms do not always guarantee an optimal solution for every problem. In some cases, a greedy approach may lead to a locally optimal solution that is not globally optimal. The lack of backtracking or reconsideration of previous choices can cause the algorithm to overlook potentially better solutions that require a more in-depth exploration of the solution space.
Decision Tree
Based on the Maze example introduced above for every position my,x reached a state in a decision tree is represented. The connection between the states is represented by the heuristic calculation h(n,k).
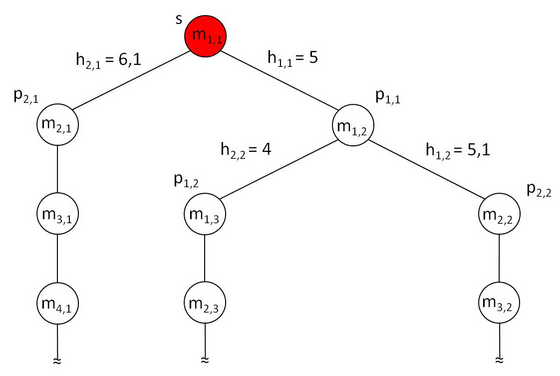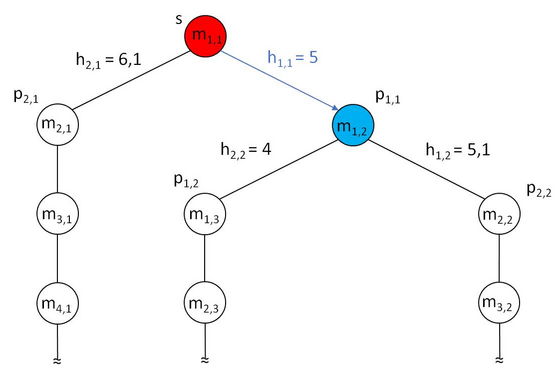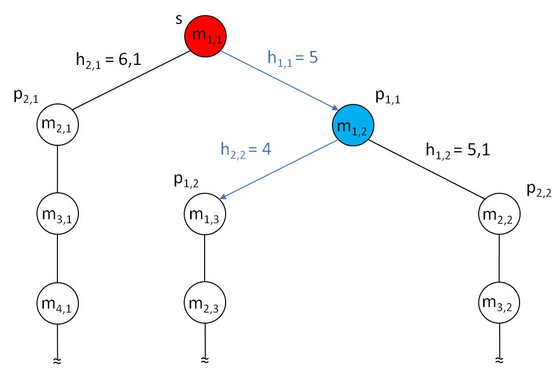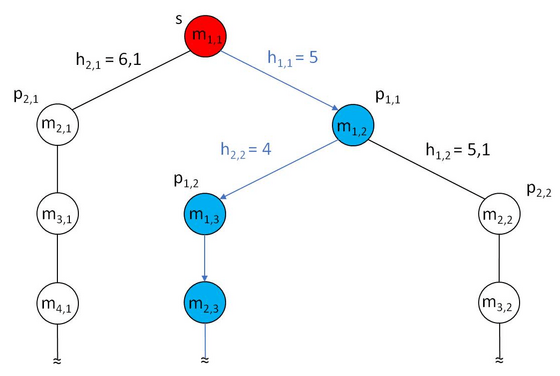
Based on the minimun heuristic result the connection is selected to move to next step. This is repeated until exit state (e) is reached.
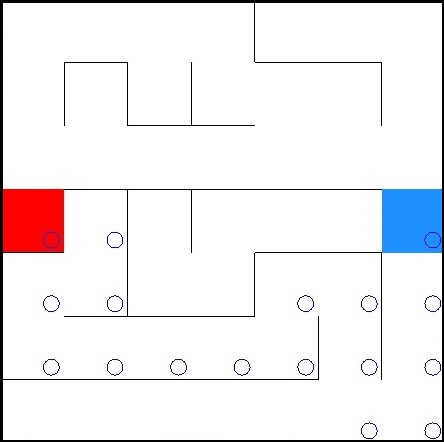
As shown above the Greedy Algorithm starts to the right based on the minimum heuristic calculation and then follows the path until exit has been found. Note that there is no backtracking to try another route. This would cost more time and sometimes even inefficient.
Optimal Solution
The Greedy algorithm doesn’t consider the effort needed to reach actual position and to reach exit finally. Thus the effort is another information which can be added to the heuristic.
f_{(k)} = h_{(k)} + c_{(k)}=\big|\vec{p}_k-\vec{e}\big|+\big|\vec{s}-\vec{p}_k\big|\\[5pt]This defines an optimal search algorithm and is named as A* algorithm (A star algorithm). So the total effort over time and steps is finally the sum of the costs (c).
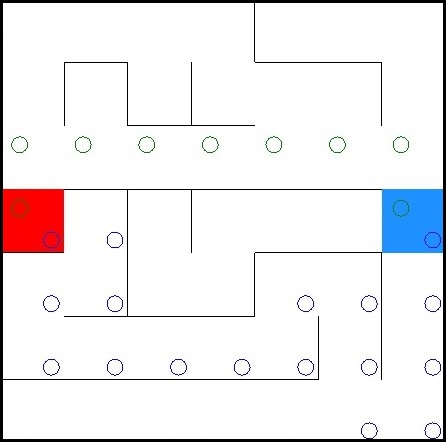
The result in opposite of the Greedy Algorithm is visible by the example used above. The path with blue circles was calculated by the Greedy Algorithm and the green circle ones by the A* Algorithm.
Implementation in C#
The following section shows the C# implementation for Greedy and A* Algorithm. The complete source code is available in Github.
There is a abstract class “Route” which provides common functions used by both algorithms except “find_children” function.
abstract class Route
{
protected PointF calcRoomPos(int room) { ... }
protected double distance(pos_t room1, pos_t room2) { ... }
protected int compareCostBySum(cost_t a, cost_t b) { ... }
protected int applicable(pos_t start, ref pos_t next, pos_t destination, ref double cost, ref double heuristic) { ... }
protected abstract int find_children(pos_t start, pos_t destination, int index);
public Route() { ... }
public void clearRoute() { ... }
public virtual void routeStart(int actR, int tarR, Size roomC, List<Door> doorL) { ... }
public virtual void routeProcess() { ... }
}This function (find_children) is implemented in separate classes for Greedy (GreedyRoute) and A* (AStarRoute) derived from base class Route based on their own heuristic calculations.
class GreedyRoute : Route
{
public GreedyRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index) { ... }
}
class AStarRoute : Route
{
public AStarRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index) { ... }
}The function “calcRoomPos” calculates the middle position of a maze field based on the field number. Here mentioned as room.
protected PointF calcRoomPos(int room)
{
PointF ret = new PointF();
ret.X = (((float)(room % rooms.Width)) * roomWidthLen) + (roomWidthLen / 2.0f);
ret.Y = (((float)(room / rooms.Height)) * roomHeightLen) + (roomHeightLen / 2.0f);
return ret;
}The distance between two maze fields e.g. actual position and exit field is calculated by theorem of pythagoras.
protected double distance(pos_t room1, pos_t room2)
{
double ret;
double x1 = room1.pos.X;
double y1 = room1.pos.Y;
double x2 = room2.pos.X;
double y2 = room2.pos.Y;
ret = Math.Sqrt(((x1 - x2) * (x1 - x2)) + ((y1 - y2) * (y1 - y2)));
return ret;
}The order of the sort algorithm to take next maze field is given by following function. Note that in case of equal costs the order of next maze field is decided by random. The variable “sum” contains in Greedy Algorithm the guess (cost from actual position to exit field) and in A* Algorithm the effort plus guess (total costs).
protected int compareCostBySum(cost_t a, cost_t b)
{
int ascend = -1;
if (a.sum > b.sum)
{
ascend = 1;
}
else
if (a.sum == b.sum)
{
//ascend = 0;
ascend = 1;
var random = new Random(Guid.NewGuid().GetHashCode());
if (random.Next(2) == 0)
{
ascend = -1;
}
}
return ascend;
}The function “applicable” checks whether next maze field is a valid field to be reached. A valid field here means a transition is possible.
protected int applicable(pos_t start, ref pos_t next, pos_t destination, ref double cost, ref double heuristic)
{
int i;
int size = doorList.Count;
if (start.room == next.room)
{
return 0;
}
for (i = 0; i < size; i++)
{
if (((doorList.ElementAt(i).Cell1 == start.room) || (doorList.ElementAt(i).Cell2 == start.room))
&&
((doorList.ElementAt(i).Cell1 == next.room) || (doorList.ElementAt(i).Cell2 == next.room)))
{
next.pos = calcRoomPos(next.room);
cost = distance(start, next);
heuristic = distance(next, destination);
return 1;
}
}
return 0;
}The route calculation will be started by “routeStart” function common for both algorithms. All variables, lists, etc. will be initialized or reset to be started from scratch.
public virtual void routeStart(int actR, int tarR, Size roomC, List<Door> doorL)
{
route_cost = 0;
route_list.Clear();
routes.Clear();
search_route_list.Clear();
cost_list.Clear();
if (tarR == 0)
{
return;
}
startRoom = actR;
actRoom = actR;
tarRoom = tarR;
rooms = roomC;
doorList = doorL;
pos_t startpos;
startpos.room = actRoom;
roomWidthLen = (100.0f / ((float)rooms.Width));
roomHeightLen = (100.0f / ((float)rooms.Height));
actPos = calcRoomPos(actRoom);
startpos.pos = actPos;
tarRoomPos.room = tarRoom;
tarPos = calcRoomPos(tarRoom);
tarRoomPos.pos = tarPos;
route_list.Add(startpos);
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = route_list.Last();
knotRoom.actualCost = 0.0f;
knotRoom.done = false;
knotRoom.childrenRooms = new List<search_route_t>();
search_route_list.Add(knotRoom);
finished = false;
}The actually algorithm is running in “routeProcess”. This function is called cyclically. It consists of a main if, else-if, else condition. The first if condition checks whether to go back from a dead end. The else-if condition is true as long as there is the exit field is not reached yet and finally in else condition the exit field was found.
public virtual void routeProcess()
{
if (search_route_list.Last().done == true)
{
route_list.RemoveAt(route_list.Count - 1);
search_route_list.RemoveAt(search_route_list.Count - 1);
if (search_route_list.Count > 0)
{
search_route_list.Last().childrenRooms.RemoveAt(search_route_list.Last().childrenRooms.Count - 1);
}
int childrensCount = 0;
if (search_route_list.Count > 0)
{
childrensCount = search_route_list.Last().childrenRooms.Count;
}
if (childrensCount > 0)
{
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = search_route_list.Last().childrenRooms.Last().actualRoom;
knotRoom.actualCost = search_route_list.Last().childrenRooms.Last().actualCost;
knotRoom.done = false;
knotRoom.childrenRooms = new List<search_route_t>();
// New active knot
search_route_list.Add(knotRoom);
search_route_list.Last().done = false;
route_list.Add(search_route_list.Last().actualRoom);
}
else
{
// No more children
bool toBeFinished = false;
if (search_route_list.Count > 0)
{
search_route_list.Last().done = true;
if (search_route_list.Last().actualRoom.room == startRoom)
{
toBeFinished = true;
}
}
else
{
toBeFinished = true;
}
if (toBeFinished == true)
{
if (routes.Count > 0)
{
// All solutions found
Debug.WriteLine("All Routes found\n");
int minRoute = 100000;
int index = 0;
for (int i = 0; i < routes.Count; i++)
{
int newMin = routes.ElementAt(i).Count;
if (newMin < minRoute)
{
minRoute = newMin;
index = i;
}
}
route_list.Clear();
route_list = routes.ElementAt(index);
finished = true;
}
else
{
Debug.WriteLine("No Routes found\n");
}
}
}
}
else
if (search_route_list.Last().actualRoom.room != tarRoom)
{
int n;
int found = 0;
cost_list.Clear();
found = find_children(search_route_list.Last().actualRoom, tarRoomPos, 0);
if (found > 0)
{
cost_list.Sort(compareCostBySum);
for (n = found - 1; n >= 0; n--)
{
search_route_t foundroom = new search_route_t();
foundroom.actualRoom = cost_list[n].room;
foundroom.actualCost = cost_list[n].value + search_route_list.Last().actualCost;
foundroom.childrenRooms = new List<search_route_t>();
search_route_list.Last().childrenRooms.Add(foundroom);
}
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = search_route_list.Last().childrenRooms.Last().actualRoom;
knotRoom.actualCost = search_route_list.Last().childrenRooms.Last().actualCost;
knotRoom.childrenRooms = new List<search_route_t>();
// New active knot
search_route_list.Add(knotRoom);
search_route_list.Last().done = false;
route_list.Add(search_route_list.Last().actualRoom);
}
else
{
// New active knot has no children
// Remove knot
search_route_list.RemoveAt(search_route_list.Count - 1);
search_route_list.Last().childrenRooms.RemoveAt(search_route_list.Last().childrenRooms.Count - 1);
route_list.RemoveAt(route_list.Count - 1);
if (search_route_list.Last().childrenRooms.Count > 0)
{
search_route_t knotRoom = new search_route_t();
knotRoom.actualRoom = search_route_list.Last().childrenRooms.Last().actualRoom;
knotRoom.actualCost = search_route_list.Last().childrenRooms.Last().actualCost;
knotRoom.childrenRooms = new List<search_route_t>();
// New active knot
search_route_list.Add(knotRoom);
search_route_list.Last().done = false;
route_list.Add(search_route_list.Last().actualRoom);
}
else
{
// No more children
search_route_list.Last().done = true;
}
}
}
else
{
routes.Add(new List<pos_t>(route_list));
route_cost = search_route_list.Last().actualCost + distance(search_route_list.ElementAt(search_route_list.Count - 1).actualRoom, tarRoomPos);
Debug.WriteLine("Route cost: " + route_cost.ToString());
for (int i = 0; i < route_list.Count; i++)
{
Debug.Write(route_list.ElementAt(i).room.ToString() + ' ');
}
Debug.WriteLine("\n");
search_route_list.Last().done = true;
}
}Coming now to Algorithm specific “find_children” implementations. The main difference is the calculation of the cost. In Greedy Algorithm the cost is defined by the distance to exit field (guess) and in A* Algorithm the cost is defined by the distance to exit field plus the effort spent from start to actual position (guess+effort).
class GreedyRoute : Route
{
public GreedyRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index)
{
int i;
double effort = 0.0;
double guess = 0.0;
int size = (rooms.Height * rooms.Width);
for (i = 0; i < size; i++)
{
pos_t next;
next.room = i + 1;
next.pos = new PointF(0, 0);
if (applicable(start, ref next, destination, ref effort, ref guess) != 0)
{
int found = 0;
for (int j = 0; j < route_list.Count; j++)
{
if (route_list.ElementAt(j).room == next.room)
{
found = 1;
break;
}
}
if (found == 0)
{
cost_t cost;
cost.room.room = next.room;
cost.room.pos = next.pos;
cost.value = effort;
cost.sum = guess;
cost_list.Add(cost);
}
}
}
return cost_list.Count;
}
}class AStarRoute : Route
{
public AStarRoute() { ... }
protected override int find_children(pos_t start, pos_t destination, int index)
{
int i;
double effort = 0.0;
double guess = 0.0;
int size = (rooms.Height * rooms.Width);
for (i = 0; i < size; i++)
{
pos_t next;
next.room = i;
next.pos = new PointF(0, 0);
if( applicable(start, ref next, destination, ref effort, ref guess) != 0)
{
int found = 0;
for (int j = 0; j < route_list.Count; j++)
{
if (route_list.ElementAt(j).room == next.room)
{
found = 1;
break;
}
}
if (found == 0)
{
cost_t cost;
cost.room.room = next.room;
cost.room.pos = next.pos;
cost.value = effort;
cost.sum = effort + guess;
cost_list.Add(cost);
}
}
}
return cost_list.Count;
}
}Conclusion
While Greedy Algorithms excel in solving certain types of problems, their use is not suitable for all situations. It is essential to carefully consider the nature of the problem at hand and whether the Greedy approach will yield the desired results.
The Greedy Algorithm is a powerful and efficient problem-solving paradigm that seeks to make locally optimal choices at each step without considering their long-term consequences. Its simplicity and speed make it an attractive choice for certain types of optimization problems. However, it is crucial to be aware of its limitations and carefully evaluate its suitability for the specific problem at hand. When used judiciously, the greedy algorithm can be a valuable tool in a computer scientist’s arsenal for tackling a wide range of computational challenges.
